How Do The Various Filters Change The Spectrum Produced By The Hydrogen Lamp?

six.3: Atomic Line Spectra and Niels Bohr

Final updated
Salvage as PDF

Page ID: 52785

Learning Objectives

Define the ground state ground state and excited land of electrons
Explain the difference between line spectra for assimilation and emission of electrons
Calculate the energy associated with the electron at specified free energy land
Calculate the energy difference with electron transition from a college energy to lower energy, and vice versa
Calculate the wavelength of light emitted as a result of a item energy transition
Differentiate between the Balmer, Lyman, and Paschen Series
Describe the limitation of the Bohr Model

Line Spectra

In that location are two types of line spectra, emission and absorption. In an emission spectra electrons are excited to an excited state by thermal or electrical ways and then relax back to a lower land and emit a photon of light at a specific energy, which is seen as at a specific wavelength. That is, electrons transfer from loftier to low energy and give off a photon of light with an energy equal to the departure in free energy betwixt the two electronic states. In an assimilation spectra the contrary occurs and a sample is radiated with white low-cal of multiple wavelengths, and if there is a wavelength of the aforementioned energy as the free energy gap between ii electronic states, that photon tin can exist absorbed as an electron goes from the lower to higher (excited) energy state. Emission is an exothermic procedure in that a photon of energy leaves the system, while absorption is an endothermic process as a photon of energy is gained by the system.

Atomic Absorption Line Spectra

The following YouTube of the Sodium Absroption Lines from the Harvard Natural Sciences Lecture Demonstrations shows how an absorption line can exist seen with rather primitive equipment.

In video \(\PageIndex{ane}\) you meet what appears to be a single line simply at that place are actually two lines known as the Sodium D-lines, at 588.9950 and 589.5924 nm. What is clear is that with very low applied science these lines can be seen, and where they occur is unique for each element.

Hydrogen's absorption line spectra is shown in Figure \(\PageIndex{ane}\). Hither nosotros see five black lines indicating that light at these wavelengths is being absorbed. The colored groundwork is light that was transmitted through the sample considering there was no allowed transition where the energy gap between two orbitals equaled the energy of the photon (h\(\nu\)) .

\(\lambda= 656nm \; \; \lambda=486nm \\ \lambda=434nm \; \ ;\lambda= 410nm \)

Figure \(\PageIndex{1}\): Hydrogen Absorption Spectra, as would be observed if a continuous spectra was passed through hydrogen gas that was not excited, forth with the 4 visible wavelengths (the line on the far left is at 397nm not really visible)

Diminutive Emission Line Spectra

In a gas belch tube energy is added to a gas which is adsorbed by electrons. These excited electrons enter high energy orbitals and and then fall back to their lower free energy and can requite off a photon of light of a specific wavelength that can be seen by a diffraction grating or prism. These type of spectra are called line spectra (in contrast to continuous spectra like the colors of the rainbow) and each chemical element has a unique line spectra that tin be used to identify it.

Figure \(\PageIndex{2}\): Prism showing light existence emitted from hydrogen beingness separated into discrete wavelengths (colors), in contrast to the continuum of white light, as in the rainbow.

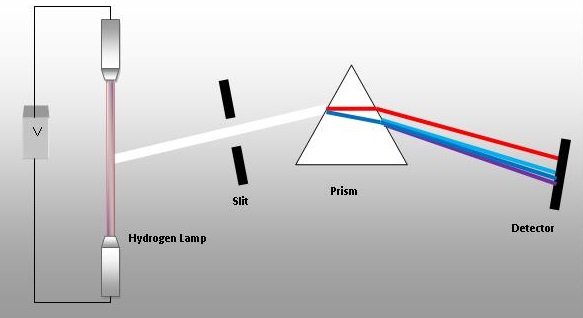
The following YouTube from Flinn Scientific goes over handling a gas discharge tube and shows the line spectra for several

clipboard_ef8a8cabb1bcbee8f6a2685accdb4f0c9

\(\lambda= 656nm \; \; \lambda=486nm \\ \lambda=434nm \; \ ;\lambda= 410nm \)

Figure \(\PageIndex{three}\): Hydrogen Emission Spectra that would be observed if the calorie-free from a gas discharge tube filled with hydrogen was passed through a filter or prisim.

Before proceeding Figures \(\PageIndex{ane}\) and \(\PageIndex{3}\) should be compared, and noted that for lines occur at the same wavelengths.

Notation: Interactive periodic table with atomic emission spectra

The following image is a link to an interactive periodic tabular array hosted by Alan Jircitano at Penn State Behrend. If you click on an element, on that table it will pull up an emission spectra, if one exits

http://chemistry.bd.psu.edu/jircitano/alphabetize.html

Spectra of Hydrogen

With simply one electron and 1 proton hydrogen is the simplest atom and early studies of its line spectra pb to some of the first theories with an experimental foundation for our understanding of the atom. The earliest equations were empirical in nature, that is, they dealt with mathematical formulas that could explain experimental observations, fifty-fifty if there was no understanding of why or what was going on. Although unknown in these early times, what nosotros at present know is that a photon of light can substitution free energy with an electron, with the electron changing orbitals, where each orbital is of a unlike free energy, and it is the difference in energy of the electron orbitals that must equal the free energy of an emitted or absorbed photon in a style that conserves free energy.

Balmer Equation

Based on empirical data measured by Anders Angstrom, Johann Balmer (1825- 1898) was a Swiss mathematician who developed an equation for computing the wavelengths of the line spectra. Information technology needs to be emphasized that although this equation could business relationship for the line spectra information technology was based on empirical (experimental) data.

\[\lambda =B\left ( \frac{n^{two}}{northward^{2}-2^{2}} \right )\]

Balmer Equation describing the visible spectrum for hydrogen atom, where B = 364.56 nm, and n is an integer larger than ii.

Rydberg Equation

Johannes Rydberg came upward with a more general equation of which the Balmer equation is a specific example for due north

\[\frac{1}{\lambda }=R\left(\frac{1}{n_{1}^{ii}}-\frac{ane}{n_{two}^{ii}}\right)\]

R is the Rydberg constant, R= 1.097x10⁷k^-i and n₁<n₂. The following image shows the line spectra in the ultraviolet (Lyman serial), visible (Balmer series) and diverse IR series that are described by the Rydberg equation.

clipboard_ece10a9473418bf27789ad01577c3a665 — Figure \(\PageIndex{4}\): The different emission transitions for the hydrogen atom. Annotation, the red ones are of low free energy (infrared) and the purple are high (ultraviolet) and the Balmer series are the ones that are visible.

Example \(\PageIndex{1}\): Algebra challenge

Can y'all derive the Balmer Equation from the Rydberg equation and using the Rydberg constant of R= 1.097x10⁷thousand^-ane come up up with a value for the Balmer constant?

Solution

B= 364.v nm. See video \(\PageIndex{4}\) for the solution of this problem

Bohr Model

The advance of the Bohr model is that it related energy to the observations Rydberg and Balmer's equations described, and it introduced the concept of the quantization of the energy level of an electron in an orbit. Where it failed was that information technology viewed electrons to reside in a classical orbit that in principle could exist defined by a radial altitude. Before reading any more spotter Video \(\PageIndex{3}\) and note that this video treats the electrons as residing in orbitals, non orbits. Orbitals will be discussed in sections half-dozen.five and six.6.

The Bohr model provides a theoretical framework for understanding line spectra. If a photon of light is absorbed, its energy (h\(\nu\)) is transferred to an electron which jumps from a low energy orbit to a high energy orbit, and the assimilation spectral lines are correlated to wavelengths associated with the frequency of that light (c=\(\lambda \nu\)). In an emission spectra electrons are excited to upper free energy states by some external energy source (thermally or electronically similar in a discharge lamp), and then the excited electron spontaneously falls back to the lower free energy footing state. This may happen through thermal or radiative ways, and if it occurs through a radiative process, a photon of the energy associated with the electronic transition is emitted and this accounts for the lines in an emission spectrum. Information technology is important to recognize that absorption is an endothermic procedure where the atom gains the energy of the photon, and emission is an exothermic process where the atom losses the free energy of the emitted photon.
clipboard_e5f8a087720c9e49f4847adcfec41139b

Figure \(\PageIndex{5}\): Energies of quantized orbitals (left) and assimilation and emission transitions of electrons between orbitals (right), with infinity correlating to ionization (removal of an electron from the atom). Those transitions between orbits and that involve the north=one land are high energy ultraviolet radiation and those involving the due north=2 to or from higher northward states are in the visible region (the n=2 to n=1 transition is ultravioloet)

The Bohr model is actually very unproblematic to empathize, in that information technology states the energy of the nth orbital is quantized, and inversely related to the square of the quantum number (northward) times the energy required to ionize the electron, that is, to remove it from an orbit. This is described by the following equation and the reason it is negative is because zero energy is that when the electron and proton are separated by infinity, and noting that to remove an electron is an endothermic process (yous add energy), ways the energy of an electron in an orbital must be less than zero..

\[E_{n}=-R_{\infty}\left(\frac{1}{northward^{2}}\right)\]

Annotation: The above equation is a course of an changed square law, except that unlike other inverse square laws, it is based on the value of an integer, \(\frac{one}{n^{2}}\), giving it values of ane,1/4,/1/9,/xvi,one/25...

Other inverse square laws are similar Coulomb's Law, \(F=k\frac{Q_{1}Q_{2}}{r^{two}}\) and Newton'due south Law \(F=G\frac{m_{1}m_{2}}{r^{2}}\) . The deviation is that the Bohr model is treating energy as a series of discrete (quantized) values inversely proportional to an integer, while Coulomb's and Newton's Police relates the strength to the inverse foursquare of the distance between 2 interacting particles, and is a continuum. That is, unlike Bohr's model, the particles tin can be separated past any distance (r is not restricted to discrete values).

\[E_{electron}= \Delta E_{n_{i}\rightarrow{n_{f}}}=E_{n_{f}}-E_{n_{i}}=-R_{\infty}\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\correct)\]

\[E_{photon}=h\nu =\frac{hc}{\lambda }\]

Absorption Spectrum

(this is endothermic and northward_f> n_i)

The energy of the photon equals the energy of the electron transition as it absorbs the energy and goes to a higher level.
\[E_{photon}=E_{electron}\]
substituting \(E_{photon} =h\nu\)

\[h\nu =E_{n_{f}}-E_{n_{i}}\]

substituting \(\nu = \frac{c}{\lambda} \;from \; c=\lambda\nu\) (eq. half-dozen.i.2)
\[\frac{hc}{\lambda }=-R_{\infty}\left(\frac{one}{n_{f}^{two}}-\frac{1}{n_{i}^{2}}\right)\]
Noting \(R_{\infty}\) is the minimum energy required to photo-ionize an electron in the lowest energy level, that is, to squirt the electron from hydrogen so it is not longer in an orbital.

\[\frac{hc}{\lambda }=-R_{\infty}\left(\frac{1}{n_{f}^{two}}-\frac{ane}{n_{i}^{2}}\correct)\]

To derive the Rydberg Equation we beginning divide past hc

\[\frac{i}{\lambda }=-\frac{R_{\infty}}{hc}\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\right)\]

Then multiply by negative i
\[\frac{1}{\lambda }=\frac{R_{\infty}}{hc}\left(\frac{one}{n_{i}^{two}}-\frac{1}{n_{f}^{2}}\right)\]

And equate the Rydberg abiding to \(R_{\infty}\)/hc

\[R=\frac{R_{\infty}}{hc}\]

gives the Rydberg Equation
\[\frac{ane}{\lambda }=R\left(\frac{1}{n_{i}^{ii}}-\frac{1}{n_{f}^{ii}}\right)\]

Notation R = 1.097x10⁷m^-ane
and is the historical Rydberg constant that predicted the wavelength of the hydrogen spectra.

What we are calling \(R_{\infty}\) is the minimum energy required to remove an electron from the ground state (lowest energy) orbital of hydrogen, and
\(R_{\infty}\) = 2.18x10^-18J

Annotation

The symbol R is often used to represent both the Rydberg constant and \(R_{\infty}\) and to know which is being defined yous need to expect at the units.

If Given R = 1.097x10^sevenm^-i, employ

\[\frac{1}{\lambda }=R\left(\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{ii}}\right)\]

If Given R = ii.18x10^-18J

\[\frac{1}{\lambda }=-\frac{R}{hc}\left(\frac{ane}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\correct)\]

noting that hc has units of \( \left (J \cdot sec \right )\left ( \frac{thousand}{sec} \right )=J \cdot m\)

Emission spectrum

In emission the system loses an energy as the photon is leaving (exothermic) and so the energy of the photon is negative (due north_i> n_f)

\[-E_{photon}=E_{electron}\]

\[-\frac{hc}{\lambda }=-R_{\infty}\left(\frac{1}{n_{f}^{two}}-\frac{one}{n_{i}^{2}}\right)\]
Noting \(R_{\infty}\) is the minimum free energy required to photo-ionize an electron in the everyman energy level, that is, to eject the electron from hydrogen so information technology is not longer in an orbital.

\[\frac{hc}{\lambda }=R_{\infty}\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{ii}}\correct)\]

To derive the Rydberg Equation we first divide by hc

\[\frac{1}{\lambda }=\frac{R_{\infty}}{hc}\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\right)\]

\[\frac{1}{\lambda }=R\left(\frac{i}{n_{f}^{2}}-\frac{one}{n_{i}^{ii}}\right)\]

Note

If yous are solving for a wavelength and you lot go a negative wavelength, you lot probably treated emission as if it was assimilation, as there is no such thing as a negatative wavelength.

Practice Problems

Example \(\PageIndex{2}\)

Using the Bohr model calculate the excited state an electron relaxes from for the blue line of the hydrogen emission spectra at \(\lambda 486\) every bit seen in Figure six.3.3.

Solution

For emission we know that \[-E_{photon}=E_{electron}\] and for visible radiation the terminal country is the n=2 state.

Using eq. 6.3.20 and solving for n_i gives:

\[n_i=\sqrt{\frac{ane}{\frac{one}{n_{f}^2}-\frac{1}{\lambda R}}}\]

noting: \(R=1.097m^{-i}=0.01097nm^{-one}\) and north_i=2 for visible radiation

gives

\[n_i=\sqrt{\frac{1}{\frac{one}{2^2}-\frac{1}{486nm\left ( 0.01907nm^{-1} \right )}}}=4\]

And so the blue line is for light emitting from an electronic transition from the n=four to n=2 state.

Practice \(\PageIndex{one}\)

What is the last quantum level in the absorption spectrum of Effigy three.6.ane for the purple ring at 434 nm?

Answer

For absorption we know that \[E_{photon}=E_{electron}\] and noting for visible radiation the initial country is the northward=2 state.

Using eq. 6.3.13 and noting for north_f.

\[n_f=\sqrt{\frac{1}{\frac{i}{n_{i}^2}-\frac{1}{\lambda R}}}\]

noting: \(R=1.097m^{-1}=0.01097nm^{-ane}\) and n_i=ii for visible radiation

gives

\[n_f=\sqrt{\frac{1}{\frac{1}{2^ii}-\frac{1}{434nm\left ( 0.01907nm^{-1} \right )}}}=5\]

So the regal absorption band at 434 nm is for light being absorbed as an electron jumps from the n=2 to the north=5 state.

Contributors and Attributions

Robert Due east. Belford (Academy of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert Eastward. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This cloth has both original contributions, and content built upon prior contributions of the LibreTexts Customs and other resources, including but not limited to:

Ronia Kattoum (UALR)
Material adopted and adjusted from Paul Flowers, et al. Open up Stax
anonymous